RESULTADOS Y REVISIÓN DE REDACCIÓN Y ORTOGRAFÍA

INTRODUCCIÓN
En esta practica utilizaremos diferentes instrumentos para Obtener el valor de la constante de elasticidad de un resorte utilizando un sistema masa-resorte dispuesto verticalmente.
Objetivos específicos

•  Desarrollar habilidades en el tratamiento gráfico de resultados experimentales. 
•  Desarrollar habilidades en la utilización de la teoría de errores. 

Cuando sobre un cuerpo se ejerce una fuerza, esta acción se transmite a la sustancia de que está compuesto, modificando la posición de los átomos, a su vez, la estructura responde con otra fuerza igual y contraria, lo cual podría interpretarse como el cumplimiento de la tercera ley de Newton (acción y reacción).  La relación entre la respuesta de una sustancia oponiéndose a su propia deformación se conoce como la Ley de Hockey, la cual se expresa matemáticamente como:  

F=  -kx 

El signo menos indica que la fuerza de restitución siempre apunta hacia la posición de equilibrio.

Datos experimentales del movimiento armónico simple (M.A.S.)

ASIGNACIÓN DE TAREAS practica #4

TAREA 1.   Introducción, desarrollo experimental y referencias NOÉ PEREZ

TAREA 2.    Resultados y revisión de redacción y ortografía ESTEBAN REQUINIVA

TAREA 3. Análisis y conclusiones  FELIPE MORALES

TAREA 4. Organización del informe final. (Aquí, deberá copiar y pegar en un archivo de

 Word las partes anteriores, para acomodar el archivo de acuerdo con las especificaciones) DANIELA GUTIERREZ

cada uno de los integrantes debe publicar una entrada con su parte del trabajo para que DANIELA lo copie y lo publique en una nueva entrada.

analisis y conclusiones.

informe #3 rozamiento

Informe Nº 3

resultados y ortografía

REVISIÓN DE ORTOGRAFÍA

INTRODUCCIÓN

El objetivo de la práctica  número 3 es el análisis de la fuerza de fricción que actúa en la superficie de dos cuerpos en contacto, ya que ningún cuerpo puede hacer fuerza sobre si mismo. analizamos las magnitudes de dicha fuerza mediante distintos ensayos, variando la masa del uno de los cuerpos y el material de la superficie en contacto. construiremos una tabla de los valores obtenidos y con ella una gráfica de masa vs newtons.

MARCO TEÓRICO

La fricción es la oposición que presenta las dos zonas de los materiales en contacto, durante el inicio, desarrollo y final del movimiento entre ellas, conlleva a consumos de energía, generación de calor, desgaste y en algunos casos a fallas catastróficas.
Los cuerpos que se mueven pueden ser sólidos, líquidos o gaseosos, o una combinación de dos o más de ellos.
la fricción se define como fuerza de fricción (F), es negativa y se opone al movimiento de traslación y refleja qué tanta energía mecánica se pierde cuando dos cuerpos inician el movimiento ó se mueven entre si y es paralela y opuesta al sentido del movimiento. Refleja que tan eficiente enérgicamente es el mecanismo durante su funcionamiento. la fuerza de fricción se calcula de la siguiente ecuación:

F = μ N (1)
Donde µ es el coeficiente de fricción estático y N es la fuerza normal.
Dado que el cuerpo está en reposo, a partir del diagrama de fuerzas se encuentran las ecuaciones:


- ∑Fx = mgsenθ – fx = 0 (3)

- ∑Fy = N − mg cosθ = 0 (4)

Si se aumenta el ángulo de inclinación gradualmente, hasta que el valor θ c ángulo al cual el objeto está a punto de iniciar su movimiento, la fuerza de fricción estática alcanza su valor máximo dado por la ecuación (1). Despejando la fricción y la normal, se tiene:

- Fsmax = mgsenθc (4)
- N= mgcos θ c
y sustituyendo en la ecuación (1) se obtiene:

µ s= tan θ c (5)

Esta ecuación, permite determinar el coeficiente de fricción estática entre dos materiales en contacto.

DESARROLLO EXPERIMENTAL

MATERIALES: 

• bloque de madera con dos superficies distintas, una en madera y otra en lija.
• juego de masas
• un dinamómetro con capacidad de 5N
• una regla de madera de un metro de longitud.
• un cronómetro.
• una rampa que se puede variar su angulo de inclinación.

METODOLOGÍA:

• se toma la superficie de madera y se pone el bloque de madera sobre la superficie.
• sobre la rampa colocamos la primera pesa (0.1N)
• luego halamos con el dinamómetro el bloque de madera, muy suavemente con una fuerza pequeña, pero paulatinamente la vamos aumentando hasta que el bloque se logre mover.
• tomamos el dato del dinamómetro (los N que marco en el instante en que se movió)
• luego repetimos este proceso con todas las masas de menor a mayor y vamos recopilando los datos en una tabla de fuerza de rozamiento vs la normal relativa en N.
• luego cambiamos la superficie de contacto con la rampa por la superficie de lija (le damos la vuelta al cubo) y hacemos otra tabla de la misma manera.
• la segunda parte de la practica consiste en variar los ángulos de la rampa.
• ponemos el cubo en la superficie de la rampa a 0º de inclinación, y vamos aumentando paulatinamente la inclinación, aumentando los grados, hasta el punto en que el bloque de madera logra deslizarse por la rampa abajo.
• tomamos el dato de cuantos grados fue necesario para que se empezara a mover el cubo. este dato se debe tomar con las dos superficies del cubo.

REFERENCIA: 

http://thales.cica.es/rd/Recursos/rd98/Fisica/02/froz.html

http://www.sc.ehu.es/sbweb/fisica/dinamica/rozamiento/general/rozamiento.htm
http://es.wikipedia.org/wiki/Coeficiente_de_rozamiento


RESULTADOS


En la tabla podemos  ver los datos de la fuerza de rozamiento estática, la fuerza de la normal que es la fuerza que hace la superficie al cuerpo (bloque de madera) y, el coeficiente de fricción, el cual es la relación que hay entre las dos magnitudes de fuerza mencionadas anteriormente.

gráfica de fuerza de rozamiento vs la fuerza normal que representa el coeficiente de fricción (madera-madera)












gráfica de fuerza de rozamiento vs la fuerza normal que representa el coeficiente de fricción (lija-madera)

Los ángulos que aparecen en la tabla son los requeridos para superar la fuerza de rozamiento estática entre las superficies mencionadas en la tabla.

diagrama de cuerpo libre

en la misma experiencia calculamos el coeficiente de fricción estática, de las mismas superficies(lija-madera)(madera-madera).

Entonces ya que tenemos el cuerpo en un plano inclinado, procedemos a hacer el diagrama de cuerpo libre como se muestra en la imagen. Luego se procede a hallar la componente del peso en el eje Y, de esta forma hallaremos la magnitud de la fricción.
Entonces para hallar la componente en Y del peso para la fuerza de fricción (lija-madera):
2N*sen(36+1/6)=1.18N
y el coeficiente de fricción de estas dos superficies seria:

Donde:

, es la fuerza paralela al plano de tangencia que intenta deslizar las superficies.

, es la fuerza normal o perpendicular al plano de tangencia.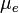

, es el coeficiente de rozamiento estático.

1.18N/2N=0.59 mayor o igual al coeficiente de rozamiento estático.

Entonces para hallar la componente en Y del peso para la fuerza de fricción (madera-madera):

2N*sen(37+1/3)=1.212N

y el coeficiente de fricción de estas dos superficies seria:
1.212N/2N=0.606 mayor o igual al coeficiente de rozamiento estático.

introducción friccion

INTRODUCCIÓN

El objetivo de la practica numero 3 es el análisis de la fuerza de fricción que actúa en la superficie de dos cuerpos en contacto, ya que ningún cuerpo puede hacer fuerza sobre si mismo. analizamos las magnitudes de dicha fuerza mediante distintos ensayos, variando la masa del uno de los cuerpos y el material de la superficie en contacto. construiremos una tabla de los valores obtenidos y con ella una gráfica de masa vs newtons.

MARCO TEÓRICO

La fricción es la oposición que presenta las dos zonas de los materiales en contacto, durante el inicio, desarrollo y final del movimiento entre ellas, conlleva a consumos de energía, generación de calor, desgaste y en algunos casos a fallas catastróficas.
Los cuerpos que se mueven pueden ser sólidos, líquidos o gaseosos, o una combinación de dos o más de ellos.
la fricción se define como fuerza de fricción (F), es negativa y se opone al movimiento de traslación y refleja qué tanta energía mecánica se pierde cuando dos cuerpos inician el movimiento ó se mueve entre si y es paralela y opuesta al sentido del movimiento. Refleja que tan eficiente enérgicamente es el mecanismo durante su funcionamiento. la fuerza de fricción se calcula de la siguiente ecuación:

F = μ N (1)
Donde µ es el coeficiente de fricción estático y N es la fuerza normal.
Dado que el objeto está en reposo, a partir del diagrama de fuerzas se encuentran las ecuaciones:


- ∑Fx = mgsenθ – fx = 0 (3)

- ∑Fy = N − mg cosθ = 0 (4)

Si se aumenta el ángulo de inclinación gradualmente, hasta que el valor θ c ángulo al cual el objeto está a punto de iniciar su movimiento, la fuerza de fricción estática alcanza su valor máximo dado por la ecuación (1). Despejando la fricción y la normal, se tiene:

- Fsmax = mgsenθc (4)
- N= mgcos θ c
y sustituyendo en la ecuación (1) se obtiene:

µ s= tan θ c (5)

Esta ecuación, permite determinar el coeficiente de fricción estática entre dos materiales en contacto.

DESARROLLO EXPERIMENTAL

MATERIALES: 

• cubo de madera con dos superficies distintas, una en madera y otra en lija, cada una en distinta cara.
• 8 pesas de diferentes masas, (desde 1N hasta 5 N)
• un dinamometro con capacidad de 10N
• una regla de madera de un metro de longitud.
• un cronometro.
• una rampa que se puede variar su angulo de inclinación.

METODOLOGÍA:

• se toma la rampa en 0º y se pone el cubo de madera sobre la rampa, con la superficie de madera en contacto con la rampa.
• sobre la rampa colocamos la primera pesa (1N)
• luego halamos con el dinamometro el cubo de madera, muy suavemente con una fuerza pequeña, pero paulatinamente la vamos aumentando hasta que el cubo se logre mover.
• tomamos el dato del dinamometro (los N que marco en el instante en que se movió)
• luego repetimos este proceso con todas las masa de menor a mayor y vamos recopilando los datos en una tabla de masa vs N.
• luego cambiamos la superficie de contacto con la rampa por la superficie de lija (le damos la vuelta al cubo) y hacemos otra tabla de la misma manera.
• la segunda parte de la practica consiste en variar los ángulos de la rampa.
• ponemos el cubo en la superficie de la rampa a 0º de inclinación, y vamos aumentando paulatinamente la inclinación, aumentando los grados, hasta el punto en que el cubo de madera logra deslizarse por la rampa abajo.
• tomamos el dato de cuantos grados fue necesario para que se empezara a mover el cubo. este dato se debe tomar con las dos superficies del cubo.

REFERENCIA: 

http://thales.cica.es/rd/Recursos/rd98/Fisica/02/froz.html

http://www.sc.ehu.es/sbweb/fisica/dinamica/rozamiento/general/rozamiento.htm

ASIGNACIÓN DE TAREAS practica #3

TAREA 1.   Introducción, desarrollo experimental y referencias FELIPE MORALES

TAREA 2.    Resultados y revisión de redacción y ortografía NOÉ PEREZ

TAREA 3. Análisis y conclusiones DANIELA GUTIERREZ

TAREA 4. Organización del informe final. (Aquí, deberá copiar y pegar en un archivo de

 Word las partes anteriores, para acomodar el archivo de acuerdo con las especificaciones)  ESTEBAN REQUINIVA

cada uno de los integrantes debe publicar una entrada con su parte del trabajo para que Esteban lo copie y lo publique en una nueva entrada.

Datos laboratorio de friccion

INFORME DE LABORATORIO N° 2

informe de laboratorio #2 (movimiento semi-parabolico)

INFORME Nº 2.docx 

ANÁLISIS Y CONCLUSIONES

ANÁLISIS

Lo que podemos ver en la gráfica de posiciones en (x) vs las posiciones en (y), es que cuando la partícula es lanzada  desde un ángulo plano, el movimiento describe una semi-parábola. La cual nos afirma que existe una fuerza gravitatoria que obliga al cuerpo a descender sin cambiar su estado de movimiento rectilíneo uniforme hasta antes de tocar el suelo. Aunque en la gráfica de posiciones de ambos ejes no nos muestra que la esfera toco el suelo ya que el método que se uso para medir las posiciones era cada 5 cm en (x) lo que no permitió medir (Y) final.

La medida del tiempo se obtuvo del supuesto de que la distancia recorrida en (y) era regida por el movimiento de caída libre, de esta forma despejamos una de las ecuaciones paramétricas  de este movimiento para obtener el tiempo correspondiente a cada valor.

la gráfica de distancia en (x) en función del tiempo nos muestra una función lineal, lo cual indica que el movimiento en x se mantuvo con una velocidad constante, ya que la pendiente de una función lineal es una constante (o en otras palabras una función lineal con pendiente cero), y la pendiente de esta gráfica es la velocidad.

En esta gráfica de posición en (y) en función

del tiempo, la altura desde la que fue lanzada la partícula se tomo como la posición inicial cero y un desplazamiento positivo hacia abajo, para obtener la visualización de una función cuadrática que nos representa analíticamente una velocidad en aumento constante, o mejor dicho  un movimiento rectilíneo uniformemente acelerado, lo que nos indica que este movimiento describe una aceleración constante en el eje y.

CONCLUSIONES

La práctica mostró que las componentes de la velocidad en el eje (x)  describen un movimiento rectilíneo uniforme, y en el eje (y) describen un movimiento rectilíneo uniformemente acelerado o más conocido como caída libre, como se esperaba que sucediera. Y demuestra que estas son las características que identifican un movimiento semi-parabólico y que esto es lo que nos ayuda a definir las ecuaciones paramétricas del movimiento.

INTRODUCCIÓN

el objetivo del la segunda practica de laboratorio es analizar el movimiento semi-parabólico, el cual tiene componentes en los ejes X y Y. analizamos el comportamiento del cuerpo en el aire en distintas distancias con respecto al origen, realizando una gráfica de X(distancia con respecto al origen) y Y(que es la altura en que se encuentre el cuerpo).

DESARROLLO EXPERIMENTAL

MATERIALES:

- rampa de madera

- mesa de apoyo

- esfera metálica

- plomada

- regla de un metro

- tira de papel blanco de un metro

- tira de papel carbón de un metro

METODOLOGÍA:

rampa en la orilla de la mesa

lo primero que debemos hacer es poner la rampa de manera fija y precisa en la orilla de la mesa con un extremo de la rampa afuera para que por ese extremo expulse la esfera.

después usamos la plomada para encontrar exactamente en que punto del suelo se forma un angulo de 90º con la salida de la rampa.

luego con este dato, construimos una linea en el piso con una marca cada 5cm. (5cm, 10cm, 15cm...)

tomamos la regla de un metro de longitud y la tira de papel blanco y la ponemos sobre la regla paralelamente, y sobre la tira de papel blanco, ponemos la tira de papel carbón y de igual manera paralela a la regla. 

luego con ayuda de la plomada ponemos la regla en la primera marca del suelo (5cm) formando un angulo de 90º entre la regla y el suelo. 

las cintas de papel deben quedar de frente a la salida de la rampa para que la esfera impacte la regla por la parte del las tiras de papel.

se realiza el lanzamiento de la esfera por la rampa una sola ves, luego se corre la regla a la siguiente marca del suelo (10cm) y se realiza el segundo lanzamiento. y así consecutivamente con todas las marcas del suelo.

es importante saber que se debe realizar un solo lanzamiento por cada una de las marcas en el suelo, y que el lanzamiento de la esfera se debe realizar siempre desde la misma altura en la rampa.

la esfera va a impactar cada ves a menor altura, de tal manera que la altura se hace 0.

cuando terminemos en cero, retiramos la cinta de papel blanco con precaución de no hacerle mas marcas con nuestros dedos, miramos los puntos que han dejado los impactos de la esfera en el papel

dibujamos un circulo en cada uno de los puntos que tenga como radio el radio de la esfera que utilizamos, en nuestro caso era de 1.115cm, luego procedemos a realizar la gráfica donde X=(a los 5 cm consecutivos del suelo) y Y(la altura que tiene la esfera en cada X ).

 de esta forma la gráfica nos mostrara la semi-parábola que describe el movimiento del cuerpo.

 REFERENCIA:
http://www.quimicayalgomas.com/fisica/tiro-oblicuo-formulas-y-ejercicios/

Laboratorio 2: movimiento semiparabolico.Datos.

Errores cometidos.

Se puede observar que en la gráfica hay unos puntos que son notorios en cuanto no permiten que se forme adecuadamente la parábola, esto se debe a que la regla no estaba formando un Angulo de 90 grados con respecto a la horizontal, ocasionando que se alteraran los datos.

Criterios adoptados.

En la toma de datos para la altura (eje Y) se tuvo en cuenta, el radio de la esfera y parte de la rampla. En la gráfica, se puede observar que no toca al eje x, puesto que el centro de la esfera no va a tocar el suelo, para ello, habría que restarle el radio, pero esto modificaría la altura.

ASIGNACIÓN DE TAREAS practica #2

TAREA 1.   Introducción, desarrollo experimental y referencias FELIPE MORALES

TAREA 2.    Resultados y revisión de redacción y ortografía DANIELA GUTIERREZ

TAREA 3. Análisis y conclusiones ESTEBAN REQUINIVA

TAREA 4. Organización del informe final. (Aquí, deberá copiar y pegar en un archivo de

 Word las partes anteriores, para acomodar el archivo de acuerdo con las especificaciones)  NOÉ PEREZ

cada uno de los integrantes debe publicar una entrada con su parte del trabajo para que Noé lo copie y lo publique en una nueva entrada.

análisis y conclusiones

análisis de los datos en un comienzo no se midió el tiempo de reacción del compañero a cargo del cronometro, a causa de esto, algunos datos del movimiento uniformemente acelerado, quedaron un poco desacordes, esto es notorio en las gráficas correspondientes a dichos movimientos, pero al hacer la tendencia de los puntos, da como resultado una curva, la cual caracteriza a este movimiento. En el movimiento rectilíneo uniforme, en el gráfico, la tendencia de los puntos,dibujan una linea recta, creciente, en la cual la pendiente de la tangente de la recta es la velocidad. conclusiones. En ambos experimentos, la inclinación de los tubos, es independiente a la magnitud de la velocidad (MRU) o la aceleración (MUA),pero estas ultimas son dependientes de en ángulo con respecto la horizontal. la inclinación es directamente proporcional a la magnitud de la velocidad o la aceleración (dependiendo del tipo de movimiento).

informe practica #1

ANALISIS Y CONCLUSIONES

MOVIMIENTO RECTILÍNIO UNIFORME
En la gráfica de posición respecto al tiempo, encontramos para este ejercicio una semejanza con una función lineal lo que nos lleva a deducir que para cada valor de (t) existe un único valor en (x).

si este movimiento nos representa una función lineal la pendiente nos representaría una constante, que en este caso seria la aceleración.

 MOVIMIENTO RECTILÍNEO UNIFORMEMENTE VARIADO

como podemos ver en la gráfica de posición respecto al tiempo, se puede denotar una semejanza geométrica con una función cuadrática. 

si lo que tenemos aquí es una función cuadrática, tendrá que haber una variación en su pendiente, por lo cual si hallamos la pendiente derivando la función nos dará una función lineal, como lo apodemos apreciar aproximadamente en el siguiente gráfico.

este gráfico de velocidad respecto al tiempo nos representa la función lineal que se deriva de la función anterior.

CONCLUSIONES

• En la practica los resultados son muy distintos a la teoria y eso es algo de lo que podemos dar por concluido de acuerdo con los resultados de la práctica.
• percibimos y observamos con los distintos experimentos que los movimientos rectilineos tienen dos grandes caracteristicas, una es el movimiento rectilíneo uniforme el cual posee un cuerpo cuando se mueve con velocidad constante de acuerdo con la pendiente de la gráfica de posicion respecto al tiempo. Y la otra caracteristica es el movimiento rectilínio uniformemente variado en el cual encontramos una velocidad que aumenta proporcionalmente, ya que la pendiente de posicion respecto al tiempo va aumentando en forma cuadrática, y que tambien posee una aceleracion constante ya que la pendiente de la función de velocidad respecto al tiempo es una constonte, pues la pendiente de una función lineal es una constante.

resultados-practica #1

RESULTADOS

Primer ejercicio de movimiento rectilíneo uniforme

En la gráfica de posición respecto al tiempo, encontramos para este ejercicio una semejanza con una función lineal lo que nos lleva a deducir que para cada valor de (t) existe un único valor en (x).

si este movimiento nos representa una función lineal la pendiente nos representaría una constante, que en este caso seria la aceleración.

Segundo ejercicio de movimiento rectilíneo uniforme con un angulo mayor.

En este ejercicio nos resulta de igual forma una función lineal así que deduciríamos que como la pendiente siempre va a ser la misma esta sera una constante.

primer ejercicio de movimiento uniformemente variado

como podemos ver en la gráfica de posición respecto al tiempo, se puede denotar una semejanza geométrica con una función cuadrática. 

si lo que tenemos aquí es una función cuadrática, tendrá que haber una variación en su pendiente, por lo cual si hallamos la pendiente derivando la función nos dará una función lineal, como lo apodemos apreciar aproximadamente en el siguiente gráfico.

este gráfico de velocidad respecto al tiempo nos representa la función lineal que se deriva de la función anterior.

segundo ejercicio de movimiento uniformemente variado con un angulo mayor

como podemos ver en la gráfica de posición respecto al tiempo, se puede denotar una aproximación geométrica con una función cuadrática la cual no es tan notable como el ejercicio anterior. 

si lo que tenemos aquí es una función cuadrática, tendrá que haber una variación en su pendiente, por lo cual si hallamos la pendiente derivando la función nos dará una función lineal, como lo apodemos apreciar aproximadamente en el siguiente gráfico.

este gráfico de velocidad respecto al tiempo nos representa la función lineal que se deriva de la función anterior.

Introducción, desarrollo experimental y referencias práctica #1

INTRODUCCIÓN

El objetivo de la práctica de laboratorio número uno, es el estudio y el análisis del movimiento rectilíneo uniforme y el movimiento rectilíneo uniformemente variado. Analizar el comportamiento de los cuerpos, mediante la sistematización de los datos tomados en dos prácticas distintas. Se estudiara el comportamiento de los cuerpos con el análisis de las gráficas de posición respecto al tiempo, y de velocidad respecto al tiempo, y así definir las ecuaciones que rigen el movimiento.

DESARROLLO EXPERIMENTAL

MOVIMIENTO RECTILÍNEO UNIFORME

MATERIALES

- tubo con burbuja: este se uso como instrumento principal de la práctica pues a la burbuja que contiene este tubo se le tomaron los datos de posición y tiempo, y por ende una velocidad.
- soporte universal: este instrumento se uso como soporte para darle una inclinación al tubo de burbuja. 

- regla: este instrumento se uso para tomar los datos de la altura del cateto opuesto al ángulo de inclinación, y para marcar las posiciones de la burbuja en su recorrido.

- cronómetro: se uso para tomar las unidades de tiempo en segundos para cada posición de la burbuja.

METODOLOGÍA

• El primer paso para instalar los instrumentos que usamos en la practica del movimiento rectilíneo uniforme es unir el soporte universal al mesón. 
• Luego ubicamos el tubo con burbuja sobre el soporte universal haciendo que forme un angulo de inclinación con respecto a la superficie del mesón.

• después se procede a calcular el ángulo que forma el tubo con la burbuja respecto del mesón, tomando las medidas de la altura y sabiendo el largo del tubo calculamos el seno del ángulo pues esta función trigonométrica es la que nos relaciona el cateto opuesto al ángulo y la hipotenusa.

• luego procedemos a tomar las medidas del tiempo que tarda la burbuja para cada desplazamiento.
• tomando cada desplazamiento en diez, veinte, treinta, cuarenta, y cincuenta tomamos para cada uno de estos, siete medidas de tiempo.

• para este ejercicio tomamos los tiempos para cada desplazamiento y lo promediamos, y hayamos la incertidumbre para cada dato usando la desviación media para datos de una misma cantidad.

• luego cambiamos el angulo de inclinación del tubo y  hacemos  el mismo procedimiento que el ejercicio anterior. 

MOVIMIENTO RECTILÍNEO UNIFORMEMENTE ACELERADO

MATERIALES
-esfera de hierro: se uso como instrumento esencial de la práctica pues a esta fue a la que le tomamos los valores de posición y tiempo.

- tubos de neón: estos se usaron como carrete para la esfera de hierro.
- soporte universal: este instrumento se uso como soporte para darle una inclinación a los tubos de neón.

- regla: este instrumento se uso para tomar los datos de la altura del cateto opuesto al ángulo de inclinación, y para marcar las posiciones de la esfera en su recorrido.

- cronómetro: se uso para tomar las unidades de tiempo en segundos para cada posición de la esfera.

METODOLOGÍA

• El primer paso para instalar los instrumentos que usamos en la practica del movimiento rectilíneo uniformemente acelerado es unir el soporte universal al mesón. 

• Luego ubicamos los tubos de neón sobre el soporte universal haciendo que forme un angulo de inclinación con respecto a la superficie del mesón.

• después se procede a calcular el ángulo que forman los tubos de neón respecto del mesón, tomando las medidas de la altura y sabiendo el largo de los tubos calculamos el seno del ángulo pues esta función trigonométrica es la que nos relaciona el cateto opuesto al ángulo y la hipotenusa.

• marcamos las medidas de longitud en los tubas de neón para facilitar la toma de las medidas.

• luego procedemos a tomar las medidas del tiempo que tarda la esfera para cada desplazamiento.

• tomando cada velocidad media de veinte en veinte desde la posición inicial cero hasta ciento sesenta. tomamos para cada uno de estos, siete medidas de tiempo.

• para este ejercicio tomamos los tiempos para cada desplazamiento y lo promediamos, y hayamos la incertidumbre para cada dato usando la desviación media para datos de una misma cantidad.

• luego cambiamos el ángulo de inclinación de los tubos y  hacemos  el mismo procedimiento que el ejercicio anterior. 

REFERENCIAS

• http://www.generadordegraficos.com/graph
• https://drive.google.com/folderview?id=0B_udmYPbu9F5clNOY084d1lYcUk&usp=sharing